Let the set
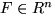 .
A
.
A 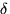 -cover of F is a countable
or finite union of non-empty subsets
-cover of F is a countable
or finite union of non-empty subsets
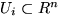 with diameter
with diameter 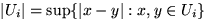 less than
less than 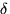 which cover F:
which cover F:
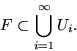
Let 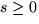 then
then
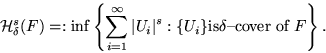
If 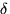 gets smaller the number of allowed covers decreases and
the infimum
gets smaller the number of allowed covers decreases and
the infimum
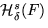 increases and has a limit for
increases and has a limit for
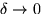 :
:
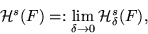
This limit exists and is called the Hausdorff measure.
If t>s and
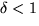 then
then
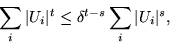
and
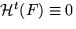 if
if
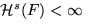 .
.
So if you explore 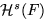 as a function of s there is
a jump from
as a function of s there is
a jump from 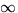 to zero at some s which is called the
Hausdorff dimension
to zero at some s which is called the
Hausdorff dimension 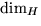 of F.
of F.
This document was generated using the
LaTeX2HTML translator Version 97.1 (release) (July 13th,
1997)
Copyright © 1993, 1994, 1995, 1996, 1997,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
From the sci.fractals FAQ:
A clear and concise (2 page) write-up of the definition of the
Hausdorff-Besicovitch dimension in MS-Word 6.0 format is available in
zip format.
hausdorff.zip (~26KB)
http://www.newciv.org/jhs/hausdorff.zip
Jürgen Dollinger
12/17/1997
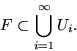
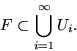
![]() then
then
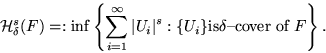
![]() gets smaller the number of allowed covers decreases and
the infimum
gets smaller the number of allowed covers decreases and
the infimum
![]() increases and has a limit for
increases and has a limit for
![]() :
:
![]()
![]() then
then
![]()
![]() as a function of s there is
a jump from
as a function of s there is
a jump from ![]() to zero at some s which is called the
Hausdorff dimension
to zero at some s which is called the
Hausdorff dimension ![]() of F.
of F.